Lineare Regression im Machine Learning: Ein Einstieg für Anfänger

25.01.2024

Zusammenfassung

Ein verständlicher Einstieg in die lineare Regression mit Modell, Kostenfunktion und Gradientenabstieg, erklärt am Beispiel von Lernstunden und Noten.

Was ist lineare Regression und warum sollten wir uns dafür interessieren?

Lineare Regression ist eine einfache Art des überwachten Lernens im Bereich des maschinellen Lernens und der Datenverarbeitung. Ihr Ziel ist es, lineare Beziehungen zwischen Eingabe- und Ausgabedaten zu finden, und basierend auf diesem linearen Modell kann sie die wahrscheinlichste Ausgabe für eine neue Eingabe vorhersagen. Die einfache Regression zeigt einige der grundlegendsten Prinzipien des maschinellen Lernens und ist ein großartiger Weg, um in dieses Gebiet einzusteigen.

Beispiel-Problem

Wir haben eine Schulklasse mit 7 verschiedenen Schülern, von denen jeder x Stunden für die letzte Klassenarbeit gelernt und dafür die Note y bekommen hat.

Nun ist die Frage: Welche Note bekommt Schüler 7 höchstwahrscheinlich, wenn er 3 Stunden gelernt hat? Vorhersagen wie diese können wir mit linearer Regression treffen.

Formel und Training

Modelldefinition

Um unsere lineare Formel aufzubauen, brauchen wir etwas Mathematik. Zunächst definieren wir die typische Formel einer linearen Geraden: y = w*x + b. Hierbei ist x die Eingabe, y die Ausgabe, w die Steigung/Gewichtung und b der y-Achsenabschnitt/Bias. Diese Formel wird Modell genannt. Um mit der Optimierung des Modells zu beginnen, müssen wir einige zufällige Werte für die Variablen w und b definieren. Es ist üblich, für beide Werte 0 als Startwert zu nehmen.

Kostenfunktion

Danach definieren wir die Kostenfunktion J:

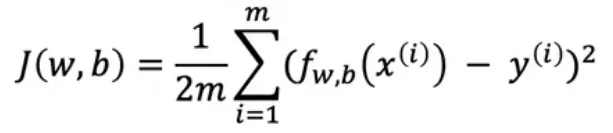
Die Kostenfunktion wird verwendet, um den "Fehler" des Modells zu berechnen. Der Fehler ist die Summe aller Differenzen zwischen den vorhergesagten Noten des Modells und den tatsächlichen Noten der Schüler. In unserem Beispiel berechnen wir folgendes:

J(0, 0) = (1/(26)) * ((4-(02+0))² + (2-(06+0))² + (3-(05+0))² + (4-(01+0))² + (1-(08+0))² + (2-(0*4+0))²). Das Ergebnis (Fehler) ist 4,17, was wirklich riesig ist, da wir noch nicht optimiert haben.

Training / Optimierung

Um unser Modell zu optimieren, brauchen wir einen Algorithmus namens Gradientenabstieg. Dieser Algorithmus wird verwendet, um die Variablen w und b zu optimieren. Das Training ist ein Prozess vieler Iterationen, in jeder Iteration optimiert der Gradientenabstieg die Variablen nur ein kleines bisschen.

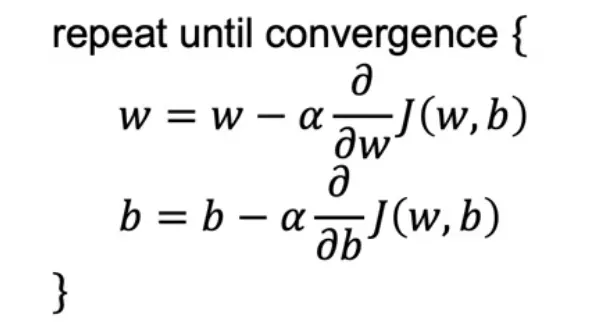
Wenn wir uns die Formel für den Gradientenabstieg zum ersten Mal ansehen, mag sie kompliziert erscheinen, aber sie ist eigentlich ziemlich unkompliziert, wenn man sie aufschlüsselt. Das Wichtigste, was man sich merken muss, ist, dass wir zwei Hauptdinge finden müssen: die besten Werte für Gewichtung (w) und Bias (b) in unserem Modell. Es ist wichtig, diese beiden Berechnungen auf ähnliche Weise zu behandeln, um genaue Ergebnisse zu erhalten.

Konzentrieren wir uns zuerst darauf, wie wir den besten Wert für die Gewichtung (w) finden:

Mit der aktuellen Gewichtung beginnen: Wir beginnen mit unserer aktuellen Schätzung für die Gewichtung, die wir 'altes w' nennen können.
Die Gewichtung anpassen: Um eine bessere Gewichtung zu finden, nehmen wir eine kleine Anpassung an 'altes w' vor. Wir tun dies, indem wir etwas davon abziehen. Dieses 'Etwas' ist eine Kombination aus zwei Faktoren: der Lernrate (α) und der Ableitung der Kostenfunktion.
Lernrate (α): Stellt euch die Lernrate wie eine Schrittgröße vor. In unserem Beispiel ist sie 0,01, was bedeutet, dass wir kleine Schritte machen. Das hilft uns, vorsichtig zu gehen und den besten Wert nicht zu verpassen.
Ableitung der Kostenfunktion: Dieser Teil sagt uns die Richtung, in die wir gehen sollten, um unseren Fehler zu reduzieren. Wenn die Ableitung positiv ist, bedeutet das, dass wir 'w' verringern müssen, um den Fehler zu reduzieren. Wenn sie negativ ist, sollten wir 'w' erhöhen.

Und was ist mit dem Bias (b)? Der Prozess ist ähnlich:

Den Bias anpassen: Genau wie bei der Gewichtung passen wir den Bias an, indem wir unsere aktuelle Schätzung, 'altes b', nehmen und eine kleine Änderung daran vornehmen.
Dieselbe Lernrate verwenden: Wir verwenden dieselbe Lernrate (0,01 in unserem Beispiel), um die Größe unseres Schritts zu bestimmen.
Die Ableitung anwenden: Wir schauen uns wieder die Ableitung der Kostenfunktion an, aber diesmal verwenden wir sie, um den Bias anzupassen.

Zusammengefasst: Wir optimieren unsere Gewichtung und unseren Bias Stück für Stück, verwenden die Lernrate, um zu kontrollieren, wie groß unsere Schritte sind, und die Ableitung der Kostenfunktion, um uns in die richtige Richtung zu führen. Dieser Prozess wird wiederholt, bis wir die besten Werte für sowohl Gewichtung als auch Bias finden, die die Vorhersagen unseres Modells so genau wie möglich machen. Diese Werte können wir dann in das Modell vom Anfang y = w * x + b einsetzen, und mit den berechneten Werten von w und b erhalten wir eine gute Vorhersage, was die vorhergesagte Ausgabe y basierend auf der Eingabe x ist.

Fazit

So, das war eine ganze Menge Mathematik. Zunächst haben wir unser Modell mit der Formel y = wx + b definiert. Dann haben wir die Kostenfunktion definiert und den Fehler berechnet. Danach sind wir zum Trainingsprozess übergegangen, wo wir die Lernrate definiert und dann die Formel zur Optimierung der Werte von w und b definiert haben.

Dies ist mein allererster Blogpost. Ich hoffe, es hat euch Spaß gemacht zu lesen.

Euer Mario 💚